— Jun 08, 2016

You know folding. You fold things everyday, clothes, paper, stacks of cash.

fold: bend something over itself so that one part of it covers another

— Dictionary.app

The act of folding is combining two parts into one. This precisely explains fold in functional programming. You fold a collection to iteratively combine its elements into a new value. Don’t be confused, fold goes by many different names in various programming languages, object-oriented and functional alike.

• accumulate(e.g. C++)
• aggregate (e.g. C#)
• inject/reduce (e.g. Ruby)

A full listing of folding functions in various languages may be seen on Wikipedia.

Despite the name, these functions all have the same basic behavior. They combine a collection by repeatedly applying some operation to its contents.

A Visual

Paper was mentioned as something you might fold. In fact it makes a practical example of programmatic folding. Consider a piece of paper containing a collection of numbers.

To combine the numbers on the paper, you might fold each pair together from the left.

Likewise, you might also fold them together from the right.

For now, consider folding from the left. In order to combine each pair of values, you must provide an operation to perform at each fold. For example, to find the sum of some numbers you might fold the collection of numbers with addition.

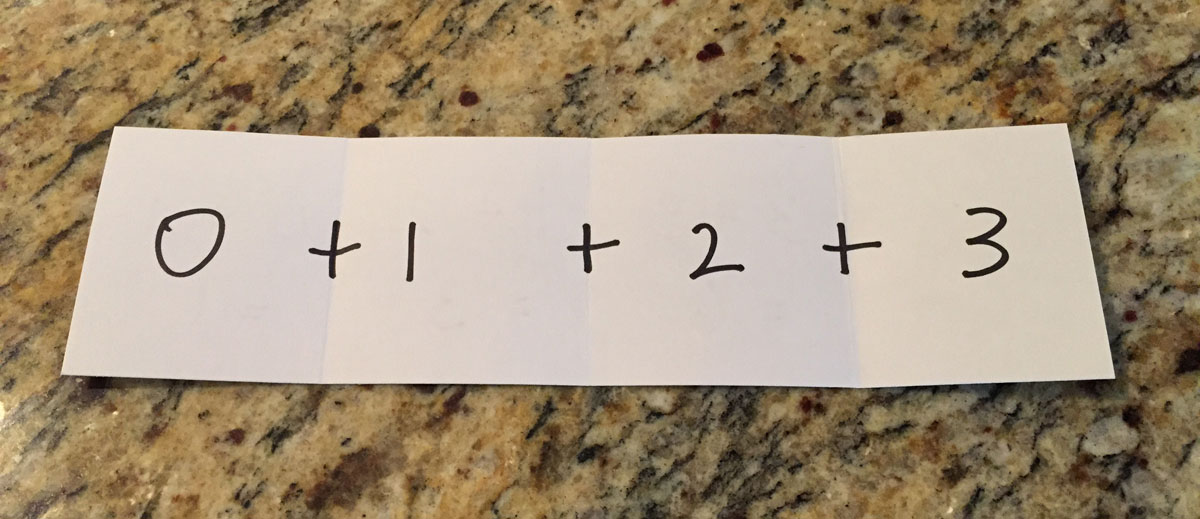
With the addition operation inserted between each pair, you can fold the collection applying the operation at each step.

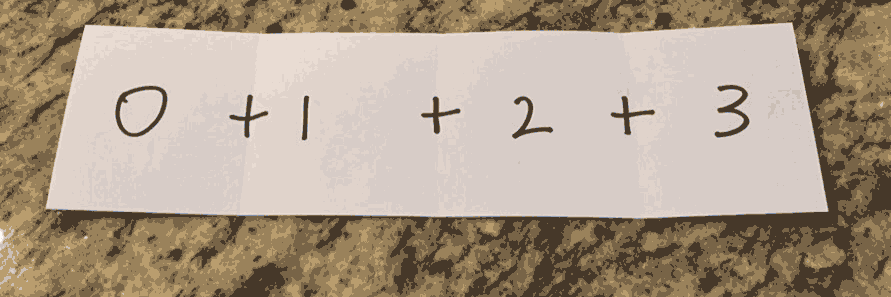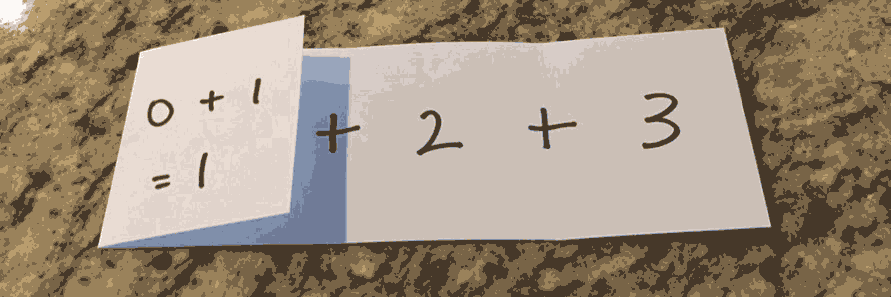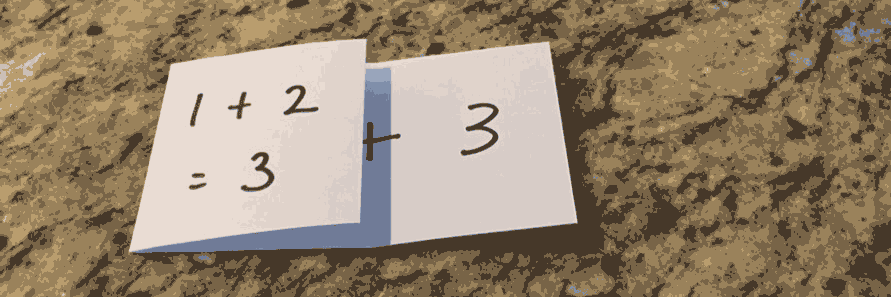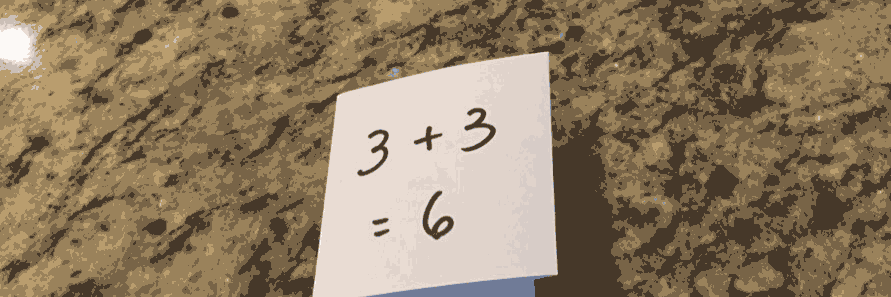
Addition is a well-known operation that most folks are familiar with, but the operation used may be arbitrarily complex as long as it has two operands and returns a value compatible with the next fold. It might even be a function itself. Folding from the left with addition might resemble the following Elixir code.

# Elixir
add = fn a, b -> a + b end
foldl([1,2,3], 0, add)

An anonymous addition function is defined and bound to the variable add. Then the fold is performed on the list of numbers [1,2,3] with the initial value 0.

Now consider a different operation. Instead of combining the collection together into a single number, the collection may be combined into a new collection. This is often referred to as “mapping”, i.e. mapping each value in the collection to a new value. The operation used by such a fold might look like this Ruby code.

# Ruby
double_shovel = ->(list, number) { list << number*2 }
foldl([1,2,3], [], double_shovel)
# => [2,4,6]

Again, a lambda (i.e. anonymous function) is defined that doubles the numbers and appends it to the array. The fold is performed with that function given an empty array ([]) as its initial value.

At each fold, the operation is applied to the last operation’s result and the next element in the collection. An initial value is provided to serve both as a starting point and as a default given an empty collection.

A Naive (Ruby) Implementation

Armed with your understanding of fold, it’s time to implement a fold_left function. Start with a method written in Ruby.

def naive_foldl(list, result, operation)
  list.each do |item|
    result = operation.(result, item)
  end
  result
end

addition = ->(a,b){ a+b }
naive_foldl(addition, 0, [1,2,3])
# => 6

Source

If you’re not used to recursion, this iteration-based implementation might be easier to grok. Starting with the second argument (result) as our initial value, the operation is iteratively applied to the result of each operation and the next element in the array. Once the entire array has been traversed, the final result is returned.

Ruby already provides a method like this in its Enumerable module, reduce.

# Ruby
[1,2,3].reduce(0) do |a,b|
  a+b
end
# => 6

Recursion

The previous implementation is considered naive, because it requires an intermediate variable result which is repeatedly assigned to throughout the run. Do not confuse naive with wrong. The solution works, but may not be the most elegant. More commonly fold is implemented using recursion. Some might argue that it is even more readable that way. Consider the following implementation of fold left written in Elixir using recursion.

def foldl([], result, _operation), do: result
def foldl([head|tail], initial, operation) do
  foldl(tail, operation.(initial, head), operation)
end

add = fn a, b -> a + b end
foldl([1,2,3], 0, add)
# => 6

Source

This implementation recursively calls foldl by applying the operation to each resulting value and the next element (“head”) of the list. In fact, similar to Ruby’s stdlib Elixir offers a very similar function by the name reduce in it’s Enum module.

Enum.reduce([1,2,3], 0, fn a, b -> a + b end)
# => 6

Does that help?

Hopefully you have found the explanation as demystifying as I have. Despite the inherent complexity of recursion and higher-order functions, the fold operation does not have to be difficult to grok. Did you find this helpful? Let me know! Also check out my other post, Folding Elixir for a little more in-depth explanation of the Elixir implementation.